Face and 2-D Mesh Animation in MPEG-4
Keywords: MPEG-4, face animation, computer graphics, deformation, VRML, speech synthesizer, electronic commerce
Abstract
This paper presents an overview of some of the synthetic visual objects supported by MPEG-4 version-1, namely animated faces and animated arbitrary 2-D uniform and Delaunay meshes. We discuss both specification and compression of face animation and 2D-mesh animation in MPEG-4. Face animation allows to animate a proprietary face model or a face model downloaded to the decoder. We also address integration of the face animation tool with the text-to-speech interface (TTSI), so that face animation can be driven by text input.
MPEG-4 is an object-based multimedia compression standard, which allows for encoding of different audio-visual objects (AVO) in the scene independently. The visual objects may have natural or synthetic content, including arbitrary shape video objects, special synthetic objects such as human face and body, and generic 2-D/3-D objects composed of primitives like rectangles, spheres, or indexed face sets, which define an object surface by means of vertices and surface patches. The synthetic visual objects are animated by transforms and special purpose animation techniques, such as face/body animation and 2D-mesh animation. MPEG-4 also provides synthetic audio tools such as structured audio tools and a text-to-speech interface (TTSI). This paper presents a detailed overview of synthetic visual objects supported by MPEG-4 version-1, namely animated faces and animated arbitrary 2-D uniform and Delaunay meshes. We also address integration of the face animation tool with the TTSI, so that face animation can be driven by text input. Body animation and 3-D mesh compression and animation will be supported in MPEG-4 version-2, and hence are not covered in this article.
The representation of synthetic visual objects in MPEG-4 is based on the prior VRML standard [13][12][11] using nodes such as Transform, which defines rotation, scale or translation of an object, and IndexedFaceSet describing 3-D shape of an object by an indexed face set. However, MPEG-4 is the first international standard that specifies a compressed binary representation of animated synthetic audio-visual objects. It is important to note that MPEG-4 only specifies the decoding of compliant bit streams in an MPEG-4 terminal. The encoders do enjoy a large degree of freedom in how to generate MPEG-4 compliant bit streams. Decoded audio-visual objects can be composed into 2D and 3D scenes using the Binary Format for Scenes (BIFS) [13], which also allows implementation of animation of objects and their properties using the BIFS-Anim node. We recommend readers to refer to an accompanying article on BIFS for the details of implementation of BIFS-Anim. Compression of still textures (images) for mapping onto 2D or 3D meshes is also covered in another accompanying article. In the following, we cover the specification and compression of face animation and 2D-mesh animation in Sections 2 and 3, respectively.
MPEG-4 foresees that talking heads will serve an important role in future customer service applications. For example, a customized agent model can be defined for games or web-based customer service applications. To this effect, MPEG-4 enables integration of face animation with multimedia communications and presentations and allows face animation over low bit rate communication channels, for point to point as well as multi-point connections with low-delay. With AT&T’s implementation of an MPEG-4 face animation system, we can animate a face models with a data rate of 300 - 2000bits/s. In many applications like Electronic Commerce, the integration of face animation and text to speech synthesizer is of special interest. MPEG-4 defines an application program interface for TTS synthesizer. Using this interface, the synthesizer can be used to provide phonemes and related timing information to the face model. The phonemes are converted into corresponding mouth shapes enabling simple talking head applications. Adding facial expressions to the talking head is achieved using bookmarks in the text. This integration allows for animated talking heads driven just by one text stream at a data rate of less than 200 bits/s [22]. Subjective tests reported in [26] show that an Electronic Commerce web site with talking faces gets higher ratings than the same web site without talking faces. In an amendment to the standard foreseen in 2000, MPEG-4 will add body animation to its tool set thus allowing the standardized animation of complete human bodies.
In the following sections, we describe how to specify and animate 3D face models, compress facial animation parameters, and integrate face animation with TTS in MPEG-4. The MPEG-4 standard allows using proprietary 3D face models that are resident at the decoder as well as transmission of face models such that the encoder can predict the quality of the presentation at the decoder. In Section 2.1, we explain how MPEG-4 specifies a 3D face model and its animation using face definition parameters (FDP) and facial animation parameters (FAP), respectively. Section 2.2 provides details on how to efficiently encode FAPs. The integration of face animation into an MPEG-4 terminal with text-to-speech capabilities is shown in Section 2.3. In Section 2.4, we describe briefly the integration of face animation with MPEG-4 systems. MPEG-4 profiles with respect to face animation are explained in Section 2.5.
MPEG-4 specifies a face model in its neutral state, a number of feature points on this neutral face as reference points, and a set of FAPs, each corresponding to a particular facial action deforming a face model in its neutral state. Deforming a neutral face model according to some specified FAP values at each time instant generates a facial animation sequence. The FAP value for a particular FAP indicates the magnitude of the corresponding action, e.g., a big versus a small smile or deformation of a mouth corner. For an MPEG-4 terminal to interpret the FAP values using its face model, it has to have predefined model specific animation rules to produce the facial action corresponding to each FAP. The terminal can either use its own animation rules or download a face model and the associated face animation tables (FAT) to have a customized animation behavior. Since the FAPs are required to animate faces of different sizes and proportions, the FAP values are defined in face animation parameter units (FAPU). The FAPU are computed from spatial distances between major facial features on the model in its neutral state.
In the following, we first describe what MPEG-4 considers to be a generic face model in its neutral state and the associated feature points. Then, we explain the facial animation parameters for this generic model. Finally, we show how to define MPEG-4 compliant face models that can be transmitted from the encoder to the decoder for animation.
As the first step, MPEG-4 defines a generic face model in its neutral state by the following properties (see Figure 1):
A FAPU and the feature points used to derive the FAPU are defined next with respect to the face in its neutral state.

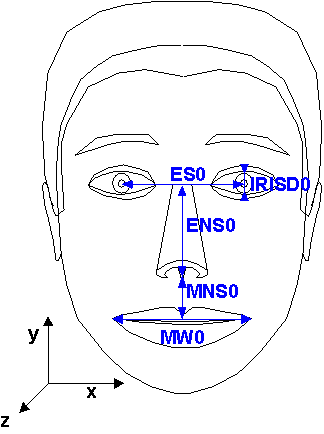
Figure 1: A face model in its neutral state and the feature points used to define FAP units (FAPU). Fractions of distances between the marked key features are used to define FAPU (from [14]).
In order to define face animation parameters for arbitrary face models, MPEG-4 defines FAPUs that serve to scale facial animation parameters for any face model. FAPUs are defined as fractions of distances between key facial features (see Figure 1). These features, such as eye separation, are defined on a face model that is in the neutral state. The FAPU allow interpretation of the FAPs on any facial model in a consistent way, producing reasonable results in terms of expression and speech pronunciation. The measurement units are shown in Table 1.
Table 1: Facial Animation Parameter Units and their definitions.
|
IRISD0 |
Iris diameter (by definition it is equal to the distance between upper ad lower eyelid) in neutral face |
IRISD = IRISD0 / 1024 |
|
ES0 |
Eye separation |
ES = ES0 / 1024 |
|
ENS0 |
Eye - nose separation |
ENS = ENS0 / 1024 |
|
MNS0 |
Mouth - nose separation |
MNS = MNS0 / 1024 |
|
MW0 |
Mouth width |
MW=MW0 / 1024 |
|
AU |
Angle unit |
10E-5 rad |
MPEG-4 specifies 84 feature points on the neutral face (see Figure 2). The main purpose of these feature points is to provide spatial references for defining FAPs. Some feature points such as the ones along the hairline are not affected by FAPs. However, they are required for defining the shape of a proprietary face model using feature points (Section 2.1.3). Feature points are arranged in groups like cheeks, eyes, and mouth. The location of these feature points has to be known for any MPEG-4 compliant face model. The feature points on the model should be located according to Figure 2 and the hints given in Table 6 in the Annex of this paper.
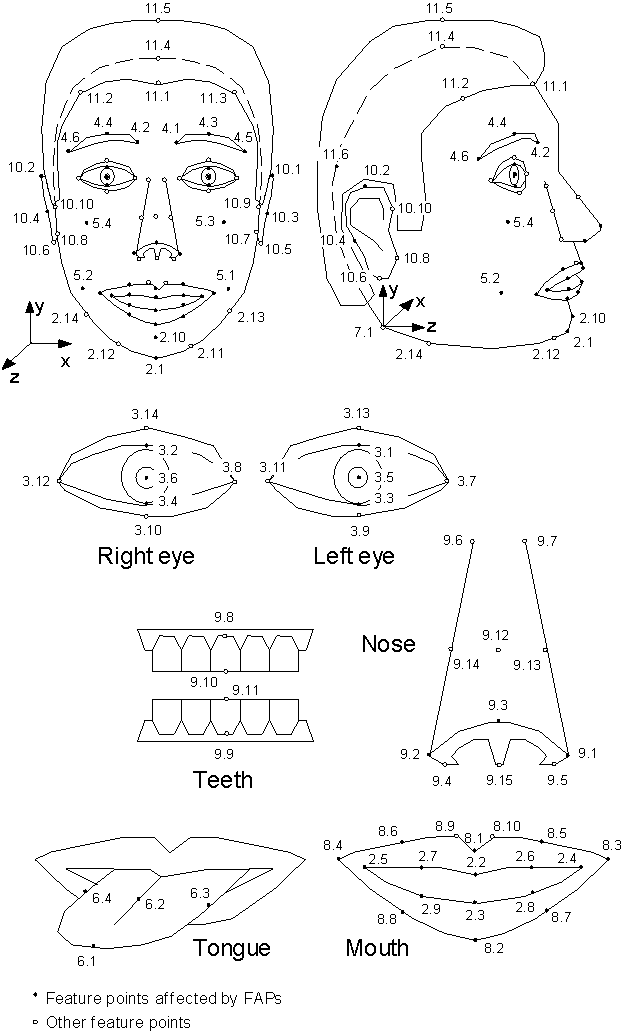
Figure 2: Feature points may be used to define the shape of a proprietary face model. The facial animation parameters are defined by motion of some of these feature points (from [14]).
The FAPs are based on the study of minimal perceptible actions and are closely related to muscle actions [2][4][9][10]. The 68 parameters are categorized into 10 groups related to parts of the face (Table 2). FAPs represent a complete set of basic facial actions including head motion, tongue, eye, and mouth control. They allow representation of natural facial expressions (see Table 7 in the Annex). For each FAP, the standard defines the appropriate FAPU, FAP group, direction of positive motion and whether the motion of the feature point is unidirectional (see FAP 3, open jaw) or bi-directional (see FAP 48, head pitch). FAPs can also be used to define facial action units [19]. Exaggerated amplitudes permit the definition of actions that are normally not possible for humans, but are desirable for cartoon-like characters.
The FAP set contains two high-level parameters, visemes and expressions (FAP group 1). A viseme (FAP 1) is a visual correlate to a phoneme. Only 14 static visemes that are clearly distinguished are included in the standard set (Table 3
). In order to allow for coarticulation of speech and mouth movement [5], the shape of the mouth of a speaking human is not only influenced by the current phoneme, but also the previous and the next phoneme. In MPEG-4, transitions from one viseme to the next are defined by blending only two visemes with a weighting factor. So far, it is not clear how this can be used for high quality visual speech animation.
The expression parameter FAP 2 defines the 6 primary facial expressions (Table 4, Figure 3). In contrast to visemes, facial expressions are animated by a value defining the excitation of the expression. Two facial expressions can be animated simultaneously with an amplitude in the range of [0-63] defined for each expression. The facial expression parameter values are defined by textual descriptions. The expression parameter allows for an efficient means of animating faces. They are high-level animation parameters. A face model designer creates them for each face model. Since they are designed as a complete expression, they allow animating unknown models with high subjective quality [21][22].
Using FAP 1 and FAP 2 together with low-level FAPs 3-68 that affect the same areas as FAP 1 and 2, may result in unexpected visual representations of the face. Generally, the lower level FAPs have priority over deformations caused by FAP 1 or 2. When specifying an expression with FAP 2, the encoder may sent an init_face bit that deforms the neutral face of the model with the expression prior to superimposing FAPs 3-68. This deformation is applied with the neutral face constraints of mouth closure, eye opening, gaze direction and head orientation. Since the encoder does not know how FAP 1 and 2 are implemented, we recommend using only those low-level FAPs that will not interfere with FAP 1 and 2.
Table 2: FAP groups
|
Group |
Number of FAPs |
|
1: visemes and expressions |
2 |
|
2: jaw, chin, inner lowerlip, cornerlips, midlip |
16 |
|
3: eyeballs, pupils, eyelids |
12 |
|
4: eyebrow |
8 |
|
5: cheeks |
4 |
|
6: tongue |
5 |
|
7: head rotation |
3 |
|
8: outer lip positions |
10 |
|
9: nose |
4 |
|
10: ears |
4 |
Table 3: Visemes and related phonemes.
|
Viseme # |
phonemes |
example |
|
0 |
none |
na |
|
1 |
p, b, m |
put, bed, mill |
|
2 |
f, v |
far, voice |
|
3 |
T,D |
think, that |
|
4 |
t, d |
tip, doll |
|
5 |
k, g |
call, gas |
|
6 |
tS, dZ, S |
chair, join, she |
|
7 |
s, z |
sir, zeal |
|
8 |
n, l |
lot, not |
|
9 |
r |
red |
|
10 |
A: |
car |
|
11 |
e |
bed |
|
12 |
I |
tip |
|
13 |
Q |
top |
|
14 |
U |
book |
Table 4: Primary facial expressions as defined for FAP 2.
|
# |
Expression name |
textual description |
|
1 |
Joy |
The eyebrows are relaxed. The mouth is open and the mouth corners pulled back toward the ears. |
|
2 |
Sadness |
The inner eyebrows are bent upward. The eyes are slightly closed. The mouth is relaxed. |
|
3 |
Anger |
The inner eyebrows are pulled downward and together. The eyes are wide open. The lips are pressed against each other or opened to expose the teeth. |
|
4 |
Fear |
The eyebrows are raised and pulled together. The inner eyebrows are bent upward. The eyes are tense and alert. |
|
5 |
Disgust |
The eyebrows and eyelids are relaxed. The upper lip is raised and curled, often asymmetrically. |
|
6 |
surprise |
The eyebrows are raised. The upper eyelids are wide open, the lower relaxed. The jaw is opened. |

Figure 3: Facial expressions.
Every MPEG-4 terminal that is able to decode FAP streams, has to provide an MPEG-4 compliant face model that it animates (Section 2.1.3.1). Usually, this is a model proprietary to the decoder. The encoder does not know about the look of the face model. Using a FDP (Face Definition Parameter) node, MPEG-4 allows the encoder to completely specify the face model to animate. This involves defining the static geometry of the face model in its neutral state using a scene graph (Section 2.1.3.3), defining the surface properties and defining the animation rules using Face Animation Tables (FAT) that specify how this model gets deformed by the facial animation parameters (Section 2.1.3.4). Alternatively, the FDP node can be used to ‘calibrate’ the proprietary face model of the decoder (Section 2.1.3.2). However, MPEG-4 does not specify how to 'calibrate' or adapt a proprietary face model.
In order for a face model to be MPEG-4 compliant, it has to be able to execute all FAPs according to Sections 2.1.1 and 2.1.2. Therefore, the face model has to have at least as many vertices as there are feature points that can be animated. Thus, an MPEG-4 compliant face model may have as little as 50 vertices. Such a model would not generate a pleasing impression. We expect to require at least 500 vertices for pleasant and reasonable face models (Figure 3).
A proprietary face model can be build in 4 steps:
Following the above steps, our face model is ready to be animated with MPEG-4 FAPs. Whenever a face model is animated, gender information is provided to the terminal. MPEG-4 does not require using a different face model for male or female gender. We recommend that the decoder reads the gender information and, at a minimum, deforms its model to be male or female. This avoids the presentation of a female face with a male voice and vice versa.
An encoder may choose to specify the location of all or some feature points. Then, the decoder is supposed to adapt its own proprietary face model such that the model conforms to the feature point positions. Since MPEG-4 does not specify any algorithm for adapting the surface of the proprietary model to the new feature point locations, we cannot specify the subjective quality of a face model after its adaptation. Face model adaptation allows also for downloading of texture maps for the face. In order to specify the mapping of the texture map onto the proprietary face model, the encoder sends texture coordinates for each feature point. Each texture coordinate defines the location of one feature point on the texture map. This does not allow for precise texture mapping at important features like eyelids or lips. Within the standard, this process of adapting the feature point locations of a proprietary face model according to encoder specifications is commonly referred to as ‘face model calibration’. As stated above, MPEG-4 does not specify any minimum quality of the adapted face model. Therefore, we prefer to name this process ‘face model adaptation’.
In [24], a method for face model adaptation is proposed using an iterative approach based on radial basis functions for scattered data interpolation. For each feature point of the proprietary model, a region of interest is defined. When a feature point moves, it deforms the model within this region of interest. In order to achieve smooth surfaces, an iterative algorithm was developed.
MPEG-4 allows for a second method of face adaptation by sending an arbitrary mesh to the decoder in addition to feature points. Whereas a possible implementation of this approach is described in [17], MPEG-4 will not mandate a specific implementation in the decoder nor will MPEG-4 define any conformance points for this approach to face model calibration. Therefore, we expect most MPEG-4 terminals not to provide this feature.
The advantage of face model adaptation over downloading a face model from the encoder to the decoder is that the decoder can adapt its potentially very sophisticated model to the desired shape. Since MPEG-4 does not define minimum qualities for proprietary face models and a good adaptation algorithm is fairly difficult to implement, we expect mostly disappointing results as also pointed out in [21]. In order to some what limit the shortcomings, we recommended that the encoder always sends the entire set of feature points for face model adaptation. Sending of partial data may result in completely unpredictable face representations. For applications that wants to specify exactly, how the contents is presented at the decoder, downloading a face model using a scene graph seems to be the preferred method (Sections 2.1.3.3 and 2.1.3.4).
In order to download a face model to the decoder, the encoder specifies the static geometry of the head model with a scene graph using MPEG-4 BIFS. For this purpose, BIFS provides the same nodes as VRML. VRML and BIFS describe scenes as a collection of nodes, arranged in a scene graph. Three types of nodes are of particular interest for the definition of a static head model. A Group node is a container for collecting child objects: it allows for building hierarchical models. For objects to move together as a group, they need to be in the same Transform group. The Transform node defines geometric affine 3D transformations like scaling, rotation and translation that are performed on its children. When Transform nodes contain other Transforms, their transformation settings have a cumulative effect. Nested Transform nodes can be used to build a transformation hierarchy. An IndexedFaceSet node defines the geometry (3D mesh) and surface attributes (color, texture) of a polygonal object. Texture maps are coded with the wavelet coder of the MPEG still image coder [14].
Figure 4 shows the simplified scene graph for a face model. Nested Transforms are used to apply rotations about the x, y, and z-axis one after another. Embedded into these global head movements are the rotations for the left and right eye. Separate IndexedFaceSets define the shape and the surface of the face, hair, tongue, teeth, left eye and right eye, thus allowing for separate texture maps. Since the face model is specified with a scene graph, this face model can be easily extended to a head and shoulder model. The surface properties of the face can be specified using colors or still images to define texture mapped models.
The shape of the face models may be generated using interactive modelers, scanners or image analysis software [16][17]
Figure 4: Simplified scene graph for a head model. The names of BIFS nodes are given in italic.
FATs define how a model is spatially deformed as a function of the amplitude of the FAPs. Three BIFS nodes provide this functionality: FaceDefTable, FaceDefTransform and FaceDefMesh. These nodes are considered to be part of the face model. Using FaceDefTransform nodes and FaceDefMesh nodes, the FaceDefTable specifies, for a FAP, which nodes of the scenegraph are animated by it and how [7].
Animation Definition for a Transform Node
If a FAP causes a transformation like rotation, translation or scale, a Transform node can describe this animation. The FaceDefTable specifies a FaceDefTransform node that defines the type of transformation and a scaling factor for the chosen transformation. During animation, the received value for the FAP, the FAPU and the scaling factor determine the actual value by which the model is transformed.
Animation Definition for an IndexedFaceSet Node
If a FAP like joy causes flexible deformation of the face model, the FaceDefTable node uses a FaceDefMesh node to define the deformation of IndexedFaceSet nodes. The animation results in updating vertex positions of the affected IndexedFaceSet nodes. Moving the affected vertices as a piece-wise linear function of FAP amplitude values approximates flexible deformations of an IndexedFaceSet. The FaceDefMesh defines for each affected vertex its own piece-wise linear function by specifying intervals of the FAP amplitude and 3D displacements for each interval (see Table 5 for an example). The VRML community started to define a Displacer Node that provides a similar functionality. However, the motion of a vertex is limited to a straight line.
If Pm is the position of the mth vertex of the IndexedFaceSet in neutral state (FAP = 0) and Dmk is the 3D displacement that defines the piecewise linear function in the kth interval, then the following algorithm is used to determine the new position P’m of the same vertex after animation with the given FAP value (Figure 5):
P’m = Pm + FAPU * ((Ik+1-0) * Dm,k + (Ik+2-Ik+1) * Dm, k+1 + …(Ij - Ij-1) * Dm, j-1 + (FAP-Ij) * Dm, j).
P’m = Pm + FAPU * (( Ij+1 - FAP) * Dm, j + (Ij+2 - Ij+1) * Dm, j+1 + … (Ik-1 - Ik-2) * Dm, k-2 + (0 - Ik-1) * Dm, k-1).
P’m = Pm + FAPU * FAP * Dm1.
Strictly speaking, these animation rules are not limited to faces. Using this technology, MPEG-4 allows for a very efficient mechanism of animating IndexedFaceSet and Transform nodes of arbitrary objects with up to 68 FAPs. In Figure 6, we see a head and shoulder model that can be animated using 68 FAPs. Obviously, the interpretation of the FAPs by the model are partially not according to the standard, since the standard does not define a means for moving an arm. Therefore, this model should only be animated by an encoder that knows the interpretation of FAPs by this model.
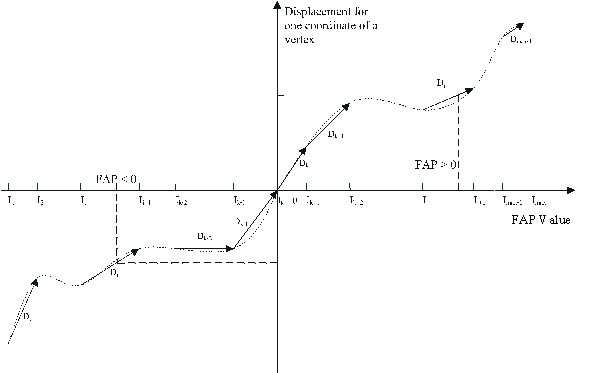 Figure 5: Piecewise linear approximation of vertex motion as a
function of the FAP Value.
Figure 5: Piecewise linear approximation of vertex motion as a
function of the FAP Value.

Figure 6: Using MPEG-4 face animation tools, face and body of this model can be downloaded and efficiently animated by the encoder that downloads the model to the decoder.
Example for a FaceDefTable
In Table 5, two FAPs are defined by children of a FaceDefTable, namely the FaceDefMesh and the FaceDefTransform: FAP 6, which stretches the left corner lip, and FAP 23, which manipulates the horizontal orientation of the left eyeball.
FAP 6 deforms the IndexedFaceSet named Face. For the piecewise-linear motion function three intervals are defined: [-1000, 0], [0, 500] and [500, 1000]. Displacements are given for the vertices with indices 50 and 51. The displacements for vertex 50 are: (1 0 0), (0.9 0 0) and (1.5 0 4), the displacements for vertex 51 are (0.8 0 0), (0.7 0 0) and (2 0 0). Given a FAP amplitude of 600, the resulting displacement for vertex 50 would be:
P’50 = P50+500*(0.9 0 0)T + 100 * (1.5 0 4)T = P50+(600 0 400)T.
FAP 23 updates the rotation field of the Transform node LeftEyeX. The rotation axis is (0, -1, 0), and the neutral angle is 0 radians. The FAP value determines the rotation angle.
Figure 8 shows 2 phases of a left eye blink (plus the neutral phase) which have been generated using a simple animation architecture [7].
The creation of the FaceDefMesh nodes for large models can be time consuming. However, the process depicted in
Figure 7
uses a FaceDefTable generator that computes these tables from a set of face models. The face model is described as a VRML file and read into the modeler. In order to design the behavior of the model for one animation parameter, the model is deformed using the tools of the modeler. The modeler may not change the topology of the model. The modeler exports the deformed model as a VRML file [12].
Figure 7: FaceDefMesh Interface - The modeler is used to generate VMRL files with the object in different animated positions. The generator computes one FaceDefMesh for each animation parameter.
The FaceDefMesh generator compares the output of the modeler with its input, the face model in its neutral state. By comparing vertex positions of the two models, the vertices affected by the newly designed animation parameter are identified. The generator computes for each affected vertex a 3D-displacement vector defining the deformation and exports this information in a FaceDefMesh table. The renderer reads the VRML file of the model and the table in order to learn the definition of the new animation parameter. Now, the renderer can use the newly defined animation as required by the animation parameters.
Table 5: Simplified example of a FaceDefMesh and a FaceDefTransform.
|
#FaceDefMesh |
|
FAP 6 (stretch left corner lip) |
|
IndexedFaceSet: Face |
|
interval borders: -1000, 0, 500, 1000 |
|
displacements: |
|
vertex 50 1 0 0, 0.9 0 0, 1.5 0 4 |
|
vertex 51 0.8 0 0, 0.7 0 0, 2 0 0 |
|
#FaceDefTransform |
|
FAP 23 (yaw left eye ball) |
|
Transform: LeftEyeX |
|
rotation scale factor: 0 -1 0 (axis) 1 (angle) |
Figure 8: Neutral state of the left eye (left) and two deformed animation phases for the eye blink (FAP 19). The FAP definition defines the motion of the eyelid in negative y-direction; the FaceDefTable defines the motion in one of the vertices of the eyelid in x and z direction. Note that positive FAP values move the vertices downwards (Table 7).
MPEG-4 provides two tools for coding of facial animation parameters. Coding of quantized and temporally predicted FAPs using an arithmetic coder allows for low delay FAP coding (Section 2.2.1). Alternatively, discrete cosine transform (DCT) coding of a sequence of FAPs introduces a larger delay but achieves higher coding efficiency (Section 2.2.2).
MPEG-4 provides a special mode (def_bit) that allows downloading definitions of expressions and visemes (FAP 1 and 2) in terms of low-level FAPs. Although the syntax for this capability is defined, MPEG-4 does not require the decoder to store a minimum number of these definitions. Therefore we recommend not using this tool until MPEG-4 provides clarifications on this tool in a potential future revision of the standard. Instead, we recommend the use of the FAP Interpolation Table (FIT) as described in Section 2.2.3.
igure 9 shows the block diagram for low delay encoding of FAPs. The first set of FAP values FAP0 at time instant 0 with is coded without prediction (intra coding). The value of a FAP at time instant k FAPk is predicted using the previously decoded value FAP'k-1. The prediction error e is quantized using a quantization step size QP that is specified in Table 7 multiplied by a quantization parameter FAP_QUANT with 0<FAP_QUANT<31. FAP_QUANT is identical for all FAP values at one time instant k. Using the FAP dependent quantization step size QP,× FAP_QUANT assures that quantization errors are subjectively evenly distributed between different FAPs. The quantized prediction error e’ is arithmetically encoded using a separate adaptive probability model for each FAP. Since the encoding of the current FAP value depends only on one previously coded FAP value, this coding scheme allows for low-delay communications. At the decoder, the received data is arithmetically decoded, dequantized and added to the previously decoded value in order to recover the encoded FAP value. When using FAP_QUANT>15, the subjective quality of the animation deteriorates significantly such that we recommend not to increase FAP_QUANT above 15 [21].
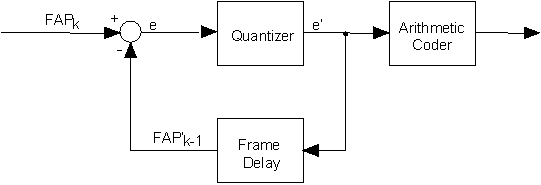
Figure 9: Block diagram of the low delay encoder for FAPs.
In order to avoid transmitting all FAPs for every frame, the encoder can transmit a mask indicating for which groups (Table 2) FAP values are transmitted. The encoder can also specify for which FAPs within a group values will be transmitted. This allows the encoder to send incomplete sets of FAPs to the decoder. FAP values that have been initialized in an intra coded FAP set are assumed to retain those values if subsequently no update is transmitted. However, the encoder can also signal to the decoder that a previously transmitted FAP value is not valid anymore.
The decoder can extrapolate values of FAPs that have been invalidated or have never been specified, in order to create a more complete set of FAPs. The standard provides only limited specifications on how the decoder is supposed to extrapolate FAP values. Examples are that if only FAPs for the left half of a face are transmitted, the corresponding FAPs of the right side have to be set such that the face moves symmetrically. If the encoder only specifies motion of the inner lip (FAP group 2), the motion of the outer lip (FAP group 8) has to be extrapolated in an unspecified way. Letting the decoder extrapolate FAP values may create unexpected results depending on the particular decoder. However, the encoder can always prevent the decoder from using extrapolation by defining all FAP values or defining FAP Interpolation Tables (Section 2.2.3).
The second tool that is provided for coding FAPs is the discrete cosine transform applied to 16 consecutive FAP values. This introduces a significant delay into the coding and decoding process. Hence, this coding method is mainly useful for applications where animation parameter streams are retrieved from a database. After computing the DCT of 16 consecutive values of one FAP, DC and AC coefficients are coded differently (Figure 10). Whereas the DC value is coded predictively using the previous DC coefficient as prediction, the AC coefficients are directly coded. The AC coefficient and the prediction error of the DC coefficient are linearly quantized. Whereas the quantizer step size can be controlled, the ratio between the quantizer step size of the DC coefficients and the AC coefficients is set to ¼. The quantized AC coefficients are encoded with one variable length code word (VLC) defining the number of zero-coefficients prior to the next non-zero coefficient and one VLC for the amplitude of this non-zero coefficient. The handling of the decoded FAPs with respect to masking and interpolation is not changed (see Section 2.2.1).
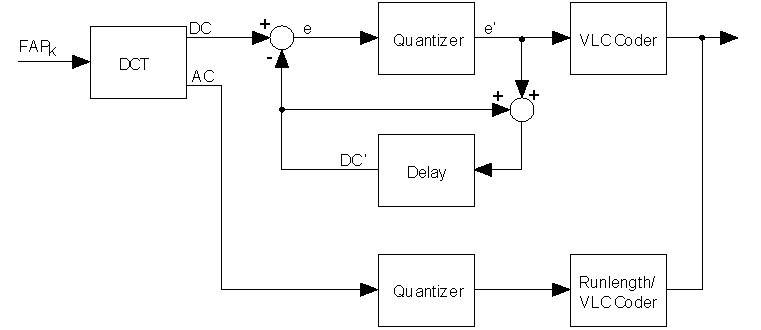
Figure 10: Block diagram of the FAP encoder using DCT. DC coefficients are predictively coded. AC coefficients are directly coded (from [23]).
Figure 11 compares the coding performance of the DCT FAP coder and the arithmetic FAP coder. The PSNR is measured by comparing the amplitude of the original and coded FAP averaging over all FAPs. This PSNR does not relate to picture quality but to the smoothness of temporal animation. In contrast to the arithmetic coder, the DCT coder is not able to code FAPs with near lossless quality. At low data rates, the DCT coder requires up to 50% less data rate than the arithmetic coder at the price of an increased coding delay. This advantage in coding efficiency disappears with increasing fidelity of the coded parameters.
Figure 11: Rate distortion performance of the arithmetic and DCT coding mode of FAPs for the sequences Marco30 (30 Hz) and Expressions (25 Hz) (from [21]).
As mentioned in Section 2.2.1, the encoder may allow the decoder to extrapolate the values of some FAPs from the transmitted FAPs [25]. Alternatively, the decoder can specify the interpolation rules using FAP interpolation tables (FIT). A FIT allows a smaller set of FAPs to be sent for a facial animation. This small set can then be used to determine the values of other FAPs, using a rational polynomial mapping between parameters. For example, the top inner lip FAPs can be sent and then used to determine the top outer lip FAPs. The inner lip FAPs would be mapped to the outer lip FAPs using a rational polynomial function that is specified in the FIT.
A FAP interpolation graph (FIG) is used to specify which FAPs are interpolated from other FAPs. The FIG is a graph with nodes and directed links. Each node contains a set of FAPs. Each link from a parent node to a child node indicates that the FAPs in a child node can be interpolated from those of the parent node. In a FIG, a FAP may appear in several nodes, and a node may have multiple parents. For a node that has multiple parent nodes, the parent nodes are ordered as 1st parent node, 2nd parent node, etc. During the interpolation process, if this child node needs to be interpolated, it is first interpolated from the 1st parent node if all FAPs in that parent node are available. Otherwise, it is interpolated from the 2nd parent node, and so on. An example of FIG is shown in Figure 12. Each node has an ID. The numerical label on each incoming link indicates the order of these links.
Each directed link in a FIG is a set of interpolation functions. Suppose F1, F2, ¼ , Fn are the FAPs in a parent set and f1, f2, ¼ , fm are the FAPs in a child set. Then, there are m interpolation functions denoted as: f1 = I1(F1, F2, …, Fn), f2 = I2(F1, F2, …, Fn), fm = Im(F1, F2, …, Fn). Each interpolation function Ik () is in the form of a rational polynomial
![]() (1)
(1)
where ![]() and
and
![]() are the numbers of polynomial products,
are the numbers of polynomial products, ![]() and
and
![]() are the coefficients of the ith product.
are the coefficients of the ith product. ![]() and
and ![]() are
the power of
are
the power of![]() in the
ith product. The encoder should send an interpolation function
table which contains all
in the
ith product. The encoder should send an interpolation function
table which contains all ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() to the decoder for each link in the FIG.
to the decoder for each link in the FIG.
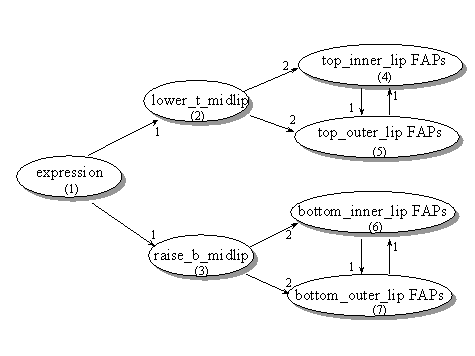
Figure 12: A FIG example for interpolating unspecified FAP values of the lip. If only the expression is defined, the FAPs get interpolated from the expression. If all inner lip FAPs are specified, they are used to interpolate the outer lip FAPs.
Here, we provide some simple examples where the use of FIT can be useful to reduce the bit rate for transmitting FAPs:
In order to specify the FITs for the examples, linear polynomials are usually sufficient. If it is desired to simulating the varying elasticity of skin for large FAP amplitudes, non-linear mappings might be useful. Following example 3, we might want the inner and outer eyebrows follow the middle eyebrow first roughly linearly and then to a lesser extend. This gives eyebrows with increasing curvature as the FAP amplitude increases.
MPEG-4 provides interfaces for a proprietary text-to-speech (TTS) synthesizer [15] that allow driving a talking head from text (see Figure 13) [5][6][8][18][1][2]. This section discusses the integration of face animation and TTS [3] allowing for animation of a talking face using a TTS synthesizer [22]. A key issue here is the synchronization of the speech stream with the FAP stream. Synchronization of a FAP stream with TTS synthesizers using the TTS Interfaces (TTSI) is only possible, if the encoder sends prosody and timing information. This is due to the fact that a conventional TTS system driven by text only behaves as an asynchronous source.
Given a TTS stream that contains text or prosody in binary form, the MPEG-4 TTSI decoder decodes the gender, text and prosody information according to the interface defined for the TTS synthesizer. The synthesizer creates speech samples that are handed to the compositor. The compositor presents audio and if required video to the user. The second output interface of the synthesizer sends the phonemes of the synthesized speech as well as start time and duration information for each phoneme to the Phoneme/Bookmark-to-FAP-Converter [22]. The converter translates the phonemes and timing information into face animation parameters that the face renderer uses in order to animate the face model. The precise method of how the converter derives visemes from phonemes is not specified by MPEG and left to the implementation of the decoder. This also allows using a coarticulation model at the decoder that uses the current, previous and next phoneme in order to derive the correct mouth shape.
Most speech synthesizers do not have a synchronous behavior. This means that the time they require to speak a sentence in not predictable. Therefore, synchronizing the output of a TTS with facial expressions defined in a FAP stream is not possible. Bookmarks in the text of the TTS are used to animate facial expressions and non-speech-related parts of the face [22]. The start time of a bookmark is derived from its position in the text. When the TTS finds a bookmark in the text it sends this bookmark to the Phoneme/Bookmark-to-FAP-Converter at the same time as it sends the first phoneme of the following word. The bookmark defines the start point and duration of the transition to a new FAP amplitude. Consequence: No additional delay, no look ahead in the bit stream but no precise timing control on when the amplitude will be reached relative to the spoken text.
An example of a TTS stream with bookmarks is given in Figure 14 [22]. The renderer will generate the visemes associated with each word, following the timing information derived by the speech synthesizer. It will also start to deform the model to generate a smile with an amplitude of 40. To simulate a more natural expression, which typically goes through three phases (onset, climax, and relax), a desired temporal behavior [20][23] for a prescribed FAP can be specified in the bookmark. Three functions are defined: A linear interpolation function and a Hermite function can be used to specify the transition of a FAP from its current value to the target value. A triangular function can be specified to linearly increase the amplitude of a FAP to the target value and to decrease it back to its starting amplitude. The bookmark also specifies the desired duration to reach the FAP value in the bookmark. If another bookmark appears before this duration, the renderer starts to deform the face according to the newly specified FAP information from the current position. This is illustrated in Figure 14 using Hermite functions.
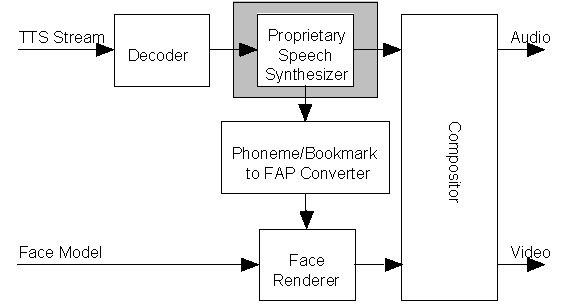
Figure 13: Block diagram showing the integration of a proprietary Text-to-Speech Synthesizer into an MPEG-4 face animation system.
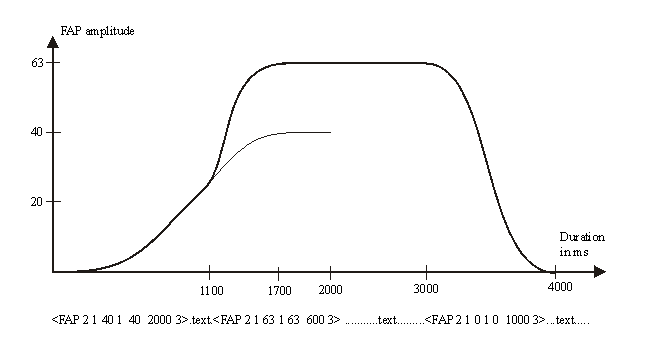
Figure 14: Example for text with bookmarks for one facial expression (joy) and the related amplitude of the animated FAP. The syntax of a bookmark is: <FAP 2 (expression) 1 (joy) amplitude 1 (joy) amplitude duration 3 (Hermite time curve)>. The amplitude of joy over time is computed according to the bookmarks (see Section 2.1.2).
In order to use face animation in the context of MPEG-4 systems, a BIFS scene graph has to be transmitted to the decoder. The minimum scene graph contains a Face node and a FAP node. The FAP decoder writes the amplitude of the FAPs into fields of the FAP node. The FAP node might have the children Viseme and Expression which are FAPs requiring a special syntax (see Section 2.1.2). This scene graph would enable an encoder to animate the proprietary face model of the decoder. If a face model is to be controlled from a TTS system, an AudioSource node is to be attached to the face node.
In order to download a face model to the decoder, the face node requires an FDP node as one of its children. This FDP node contains the position of the feature points in the downloaded model, the scene graph of the model and the FaceDefTable, FaceDefMesh and FaceDefTransform nodes required to define the action caused by FAPs. Figure 15 shows how these nodes relate to each other.
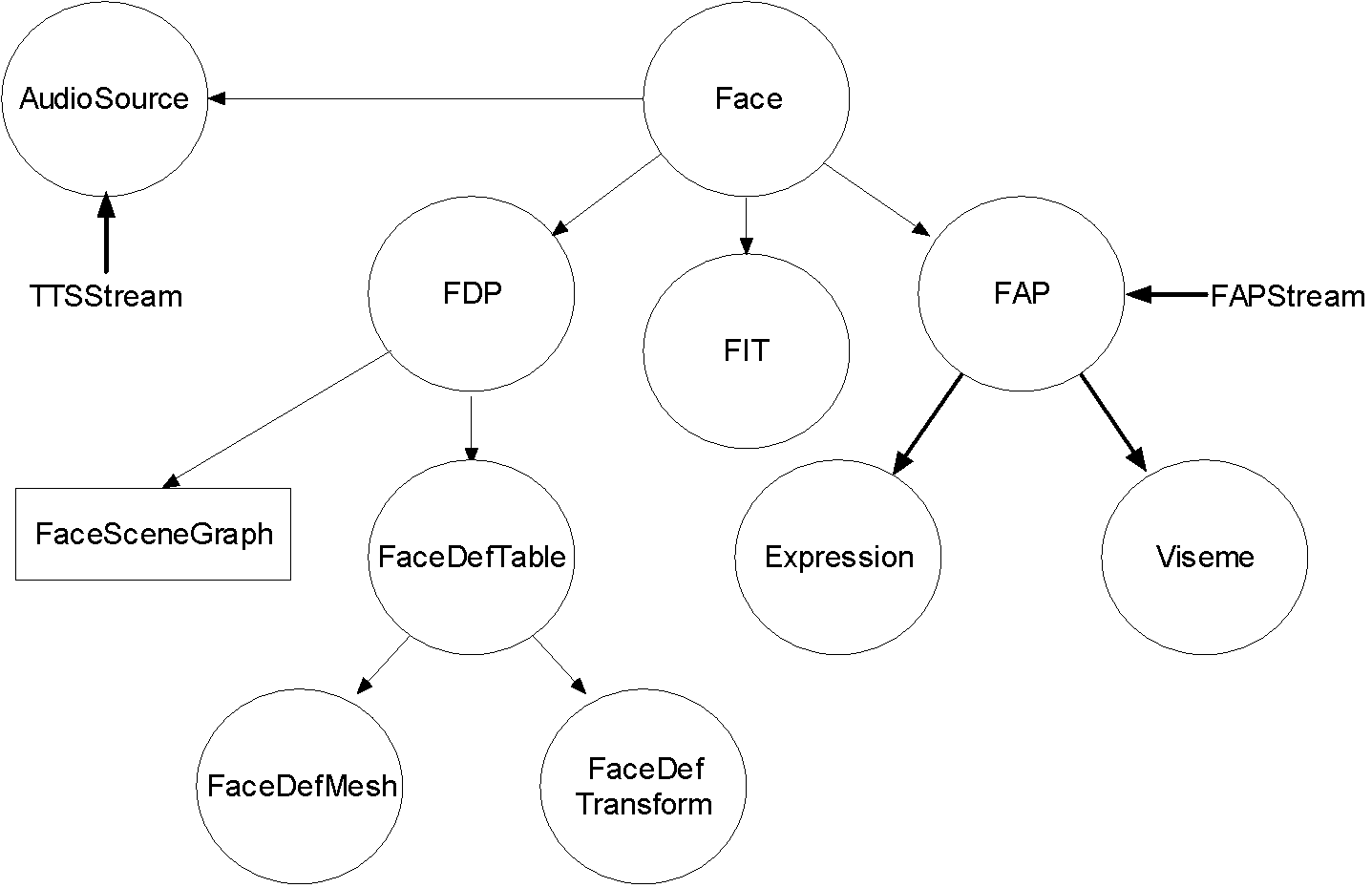
Figure 15: Nodes of a BIFS scene graph that are used to describe and animate a face. The FaceSceneGraph contains the scene graph of the static face. Here, it is assumed that the streams are already decoded.
MPEG-4 defines profiles to which decoders have to conform. A profile consists of objects defining the tools of the profile. Levels of a profile and object put performance and parameter limits on the tools. MPEG-4 Audio, Visual and Systems define parts of face animation.
In Visual, the neutral face with its feature points and FAPs, the coding of FAPs as well as the Phoneme/Bookmark-to-FAP-Converter with its interface to TTSI are defined. The corresponding object type is called Simple Face. The Simple Face object allows animating a proprietary face model using a FAP stream or from a TTSI provided that the terminal supports MPEG-4 audio. Two levels are defined for this object: At level 1, it requires to animate one face model with a maximum bit rate of 16 kbit/s and a render frame rate of at least 15 Hz. At level 2, up to 4 faces can be animated with a total bit rate not to exceed 32 kbit/s and a render frame rate of 60 Hz shareable between faces. This Simple Face object is included in the following visual profiles: Hybrid, Basic Animated Texture, and Simple FA (Face Animation). Whereas the Simple FA requires only face animation capabilities, Basic Animated Texture adds scaleable texture coding and mesh-based animation of these textures. The Hybrid profile adds video decoding according to the Core profile (video and binary shape) [14].
In MPEG-4 Audio, the TTSI with the bookmark identifiers for face animation as well as the interface to the Phoneme/Bookmark-to-FAP-converter is defined. It is part of all Audio profiles. Using a TTS, any Audio profile and a Visual profile containing the Face object allows to define interactive services with face animation at extremely low data rates. Without using a TTS, any Audio profile and a Visual profile containing the Face object allows to play speech and animate the proprietary face model.
In order to enable the specification of the face, the BIFS node FDP and its children have to be transmitted. This is possible for terminals that support the Complete Scene Graph profile and the Complete Graphics profile.
MPEG-4 version-1 supports 2D uniform or content-based (nonuniform) Delaunay triangular mesh representation of arbitrary visual objects, that includes an efficient method for animation of such meshes. A simplified block diagram of an MPEG-4 encoder/decoder supporting the 2D-mesh object is depicted in Figure 16, where the 2D-mesh object can be used together with a video object or a still-texture object encoder/decoder. We present the basic concepts of 2D-mesh representation and animation in Section 3.1. Mesh analysis, discussed in Section 3.2, refers to design or specification of 2D mesh data for video object editing or still-texture animation. Section 3.3 describes 2D-mesh object coding in detail. Finally, applications of 2D mesh in video object editing and still texture animation are presented in Section 3.4.
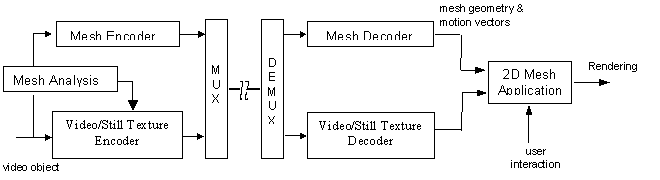
Figure 16: Simplified architecture of an encoder/decoder supporting the 2D-mesh object. Mesh analysis module extracts the 2D mesh data, which is then encoded by the mesh encoder. The coded mesh representation is embedded in a BIFS elementary stream. At the receiver, the 2D-mesh decoder is invoked automatically by the BIFS-Anim node.
A 2D triangular mesh (or a mesh object plane) is a planar graph that tessellates (partitions) a video object plane or its bounding box into triangular patches. The vertices of each patch are called node points. A 2D mesh object, which consists of a sequence of mesh object planes (MOPs), is compactly represented by mesh geometry at some key (intra) MOPs and mesh motion vectors at all other (inter) MOPs. The mesh geometry refers to the location of the node points on the key mesh object planes. 2D mesh animation is accomplished by propagating the 2D mesh defined on key MOPs using one motion vector per node point per object plane until the next key MOP. Both mesh geometry and motion (animation) information are predictively coded for an efficient binary representation. The mesh topology is always either uniform or Delaunay, hence there is no need for topology compression. (The reader is referred to [28] for an introduction to Delaunay meshes.)
Mesh-based motion modeling differs from block-based motion modeling (that is used in natural video object coding) in that the triangular patches overlap neither in the reference frame nor in the current frame. Instead, triangular patches in the current frame are mapped onto triangular patches in the reference frame, and the texture inside each patch in the reference frame is warped onto the current frame using a parametric mapping, such as affine mapping, as a function of the node point motion vectors. This process is called texture mapping, which is an integral part of mesh animation. The affine mapping between coordinates (x’,y’) at time t’ and (x, y ) at time t is given by [27]
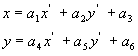 (2)
(2)
where ai are the affine motion parameters. The six degrees of freedom in the affine mapping matches that of warping a triangle by the motion vectors of its three vertices (with two degrees of freedom in each). Furthermore, if proper constraints are imposed in parameter (node motion vector) estimation, an affine transform can guarantee the continuity of the mapping across the boundaries of adjacent triangles. Thus, 2D mesh modeling corresponds to non-uniform sampling of the motion field at a number of salient feature points (node points), from which a continuous, piece-wise affine motion field can be reconstructed. The fact that the mesh structure constrains movements of adjacent image patches has certain advantages and disadvantages: Meshes are well-suited to represent mildly deformable but spatially continuous motion fields. However, they do not allow discontinuities in the motion field; thus, cannot easily accommodate articulated motions and self-occlusions.
The design of the mesh data associated with a video object or animation is an encoder issue, and hence is not normative. This section discusses an example procedure for the reader’s information, where we design either uniform or content-based meshes for intra MOPs and track them to determine the inter MOPs. The block diagram of the procedure is depicted in Figure 17. The first box is explained in Section 3.2.1, and the next four in Section 3.2.2.
Figure 17: The 2D mesh design and tracking procedure. The feedback loop increments the frame counter. The process is re-initialized (i.e., a new intra MOP is inserted) if model failure region exceeds a threshold or a scene change is detected.
Intra meshes are either uniform or content-based. A uniform mesh is designed over a rectangular region, which is generally the bounding box of the VOP. It is specified in terms of five parameters: the number of nodes in the horizontal and vertical directions, the horizontal and vertical dimension of each rectangular cell in half pixel units, and the triangle split code that specifies how each cell is divided into two triangles (see Section 3.3.1.1). As a rule of thumb, we target the total number of triangles over the bounding box to be equal to that of the macroblocks that would be obtained in natural VOP coding. A content-based mesh may be designed to fit exactly on the corresponding VOP. The procedure consists of three steps: i) Approximation of the VOP contour by a polygon through selection of Nb boundary node points; ii) selection of Ni interior node points; and iii) Delaunay triangulation to define the mesh topology. There are various methods for approximation of arbitrary shaped contours by polygons [33][35]. Interior node points may be selected to coincide with high-gradient points or corner points within the VOP boundary [33]. An example of a content-based mesh is depicted in Figure 18.

Figure 18: A content-based mesh designed for the "Bream" video object.
Motion data of the 2D mesh may represent the motion of a real video object (for natural video object compression and manipulation applications) or may be synthetic (for animation of a still texture map). In the former case, the motion of a natural video object may be estimated by forward mesh tracking. The latter requires special purpose tools and/or artistic skills. In forward mesh tracking, we search in the current video object plane for the best matching locations of the node points of the previous (intra or inter) mesh, thus tracking image features until the next intra MOP. The procedure applies for both uniform and content-based meshes.
Various techniques have been proposed for node motion estimation for forward mesh tracking. The simplest method is to form blocks that are centered around the node points and then employ a closed-form solution or block-matching to find motion vectors at the node points independently [27][29]. Alternatively, hexagonal matching [30] and closed-form matching [31] techniques find the optimal motion vector at each node under the parametric warping of all patches surrounding the node while enforcing mesh connectivity constraints at the expense of more computational complexity. Another method is iterative gradient-based optimization of node point locations, taking into account image features and mesh deformation criteria[32]. Hierarchical tracking methods may provide significantly improved performance and robustness in enforcing constraints to avoid foldovers [34][36]. We also recently proposed a semi-automatic (interactive) tool for accurate mesh object tracking [37].
Mesh data consists of a list of node locations (xn, yn) where n is the node index (n=0,¼ ,N-1) and a list of triangles tm where m is the triangle index (m = 0, ..., M-1). Each triangle tm is specified by a triplet <i, j, k> of the indices of the node points that are the vertices of that triangle. The syntax of the compressed binary representation of intra and inter MOPs and the semantics of the decoding process is normative in MPEG-4. Each MOP has a flag that specifies whether the data that follows is geometry data (intra MOP) or motion data (inter MOP). A block diagram of the decoding process is shown in Figure 19. Mesh geometry decoding computes the node point locations and reconstructs a triangular mesh from them. Mesh motion decoding computes the node motion vectors and applies them to the node points of the previous mesh to reconstruct the current mesh. The reconstructed mesh is stored in the mesh data memory, so that it can be used in motion decoding of the next MOP. In the following, we first describe the decoding of mesh geometry, and then the mesh motion. We assume a pixel-based 2D coordinate system, where the x-axis points to the right from the origin, and the y-axis points down from the origin.
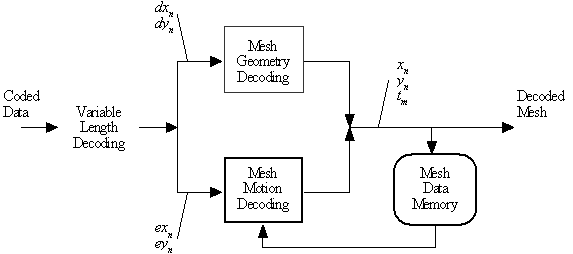
Figure 19: Simplified block diagram of 2D Mesh Object decoding.
The flag mesh_type_code specifies whether the topology of an intra MOP is uniform or Delaunay. In either case, the coded geometry information, described in detail in the following, defines the 2D mesh uniquely so that there is no need for explicit topology compression.
A 2D uniform mesh can be viewed as a set of rectangular cells, where each rectangle is split into two triangles. Five parameters are used to specify the node point locations and topology of a uniform mesh. The top-left node point of the mesh always coincides with the origin of a local coordinate system. The first two parameters specify the number of nodes in the horizontal and vertical direction of the mesh, respectively. The next two parameters specify the horizontal and vertical size of each rectangular cell in half pixel units. This completes the layout and dimensions of the mesh. The last parameter specifies how each rectangle is split to form two triangles: four choices are allowed as illustrated in Figure 20. An example of a 2D uniform mesh is given in Figure 21.
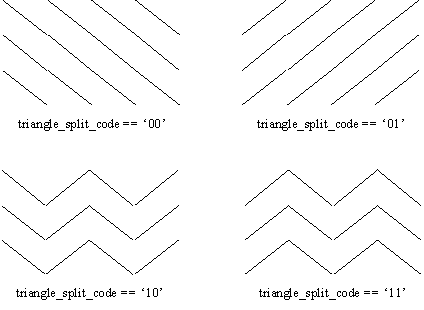
Figure 20: Types of uniform mesh topology: Code 00 - top-left to right bottom; Code 01 - bottom-left to top right; Code 10 – alternate between top-left to bottom-right and bottom-left to top-right; Code 11 – alternate between bottom-left to top-right and top-left to bottom-right.
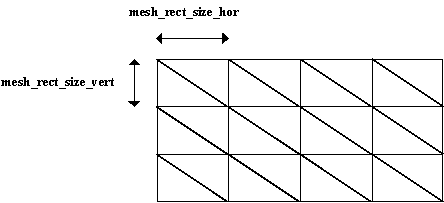
Figure 21: Example of a uniform 2D mesh specified by five parameters, where nr_mesh_nodes_hor is equal to 5, nr_mesh_nodes_vert is equal to 4, mesh_rect_size_hor and mesh_rect_size vert are specified as shown, and the triangle_split_code is equal to ‘00’.
A 2D Delaunay mesh is specified by the following
parameters: i) The total number of node points N; ii) the number of
node points Nb that are on the boundary of the mesh; and
iii) the coordinates ![]() , n=0, ¼ , N-1, of all node
points. The origin of the local coordinate system is assumed to be at the
top left corner of the bounding box of the mesh. Note that the number of
nodes in the interior of the mesh Ni can be computed
as
, n=0, ¼ , N-1, of all node
points. The origin of the local coordinate system is assumed to be at the
top left corner of the bounding box of the mesh. Note that the number of
nodes in the interior of the mesh Ni can be computed
as
![]() (3)
(3)
The first node point, ![]() , is decoded directly, where the coordinates
, is decoded directly, where the coordinates ![]() and
and ![]() are specified with respect to the origin of the local coordinate
system. All other node points are computed by adding the decoded values
are specified with respect to the origin of the local coordinate
system. All other node points are computed by adding the decoded values
![]() and
and ![]() to the x- and y-coordinates, respectively, of the last decoded node point
as follows
to the x- and y-coordinates, respectively, of the last decoded node point
as follows
![]() (4)
(4)
The first Nb node point coordinates that are encoded/decoded must correspond to the boundary nodes in order to allow their identification without additional overhead. Thus, after receiving the first Nb locations, the decoder can reconstruct the boundary of the mesh by connecting each pair of successive boundary nodes, as well as the first and the last, by straight-line edge segments. This is illustrated with an example in Figure 22.
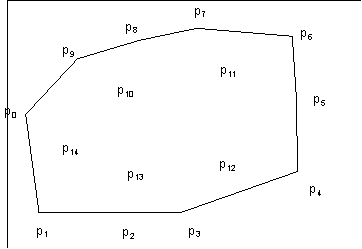
Figure 22: Decoded node points and reconstruction of mesh boundary.
The next Ni coordinate values define
the interior node points. Finally, the mesh is reconstructed by applying
constrained Delaunay triangulation to all node points, where the boundary
polygon forms the constraint. Constrained triangulation of node points
![]() contains triangles only to the interior of the region defined by the
boundary segments. Furthermore, each triangle
contains triangles only to the interior of the region defined by the
boundary segments. Furthermore, each triangle ![]() of a constrained Delaunay triangulation satisfies the property
that the circumcircle of
of a constrained Delaunay triangulation satisfies the property
that the circumcircle of ![]() does not contain any node point
does not contain any node point ![]() visible from all three vertices of
visible from all three vertices of ![]() . A node point is visible from another node point if a straight
line between them falls entirely inside or exactly on the constraining
polygonal boundary. An example of a mesh obtained by constrained
triangulation of the node points in Figure 22 is shown in Figure
23.
. A node point is visible from another node point if a straight
line between them falls entirely inside or exactly on the constraining
polygonal boundary. An example of a mesh obtained by constrained
triangulation of the node points in Figure 22 is shown in Figure
23.
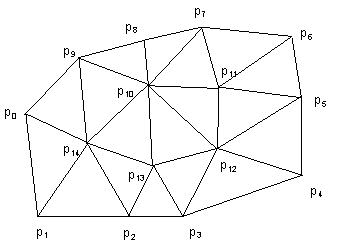
Figure 23: Decoded triangular mesh obtained by constrained Delaunay triangulation.
An inter MOP is defined by a set of 2D motion vectors
![]() that are associated with each node point
that are associated with each node point ![]() of the previous MOP. We can then reconstruct the locations of node points
in the current MOP by propagating the corresponding node
of the previous MOP. We can then reconstruct the locations of node points
in the current MOP by propagating the corresponding node ![]() of the previous MOP. The triangular topology of the mesh remains
the same until the next intra MOP. Node point motion vectors are decoded
predictively, i.e., the components of each motion vector are
predicted using those of two previously decoded node points determined
according to a breadth-first traversal as described in Section 3.3.2.1.
Section 3.3.2.2 describes the prediction process.
of the previous MOP. The triangular topology of the mesh remains
the same until the next intra MOP. Node point motion vectors are decoded
predictively, i.e., the components of each motion vector are
predicted using those of two previously decoded node points determined
according to a breadth-first traversal as described in Section 3.3.2.1.
Section 3.3.2.2 describes the prediction process.
The order in which the motion vector data is encoded/decoded is defined by a breadth-first traversal of the triangles, which depends only on the topology of the mesh. Hence, the breadth-first traversal needs to be computed once (and stored in the mesh data memory) for every intra MOP as follows:
The mesh motion bitstream is composed of prediction
error vectors ![]() , whose components are variable length coded. The ordering of
the triangles defines the order in which the motion vector data of each
node point is encoded/decoded, as described in the following. First,
motion vector data for the top-left node n0 of the
mesh is retrieved from the bitstream. No prediction can be used in
coding the motion vector of n0. Hence,
, whose components are variable length coded. The ordering of
the triangles defines the order in which the motion vector data of each
node point is encoded/decoded, as described in the following. First,
motion vector data for the top-left node n0 of the
mesh is retrieved from the bitstream. No prediction can be used in
coding the motion vector of n0. Hence,
![]() (5)
(5)
Then, the prediction error vector en1 for the next clockwise node on the boundary with respect to the top-left node is retrieved from the bitstream. Note that only vn0 can be used to predict vn1. That is,
![]() (6)
(6)
We mark these first two nodes (that form the base edge
of the initial triangle) with the label ‘done’. At this point the two
nodes on the base edge of any triangle in the sequential order as
defined in Section 3.3.2.1 are guaranteed to be labeled ‘done’
(indicating that their motion vectors have already been decoded and may
be used as predictors) when we reach that triangle. Then, for each
triangle, the motion vectors of the two nodes of the base edge are used
to form a prediction for the motion vector of the third node. If that
third node is not already labeled ‘done’, the prediction vector ![]() is computed by averaging the two motion vectors, as
follows:
is computed by averaging the two motion vectors, as
follows:
![]() (7)
(7)
and its motion vector is given by
![]() (8)
(8)
Consequently, the third node is also labeled ‘done’. If
the third node is already labeled ‘done’, then it is simply ignored and
we proceed to the next triangle. Note that the prediction error vector
is specified only for node points with a nonzero motion vector.
Otherwise, the motion vector is simply ![]() . Finally, the horizontal and vertical components of mesh node
motion vectors are processed to lie within a certain range, as in the
case of video block-motion vectors.
. Finally, the horizontal and vertical components of mesh node
motion vectors are processed to lie within a certain range, as in the
case of video block-motion vectors.
An example of breadth-first traversal for motion vector prediction is shown in Figure 24. The figure on the left shows the traversal after five triangles have been labeled, which determines the ordering of the motion vectors of six node points (marked with a box). The triangle with the label ‘3’ is the ‘current triangle’; the base edge is ‘b’; and the right- and left-edges are denoted by ‘r’ and ‘l’, respectively. The next two triangles that will be labeled are the triangles sharing the right and. left edges with the current triangle. After those two, the triangle that is labeled ‘4’ will be the next ‘current triangle.’ The figure on the right shows the final result, illustrating transitions between triangles and the final ordering of the node points for motion vector encoding/decoding.
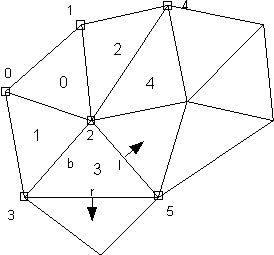
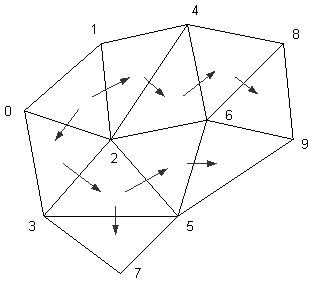
Figure 24: Example for the breadth-first traversal of the triangles of a 2D mesh.
2D mesh geometry and motion data are passed on to an IndexedFaceSet2D node using the BIFS animation-stream for rendering and/or texture mapping (see the paper on BIFS in this issue). BIFS animation is a general framework for streaming parameters to certain fields of some BIFS nodes. Suppose a node (describing an object) is below a Transform node in the scene description tree. We can then animate the position of this object using BIFS-Anim by streaming a sequence of x, y, z positions to the 'translation' field of the Transform node. In this case, the x, y, z positions are quantized and encoded by an arithmetic coder. Both 2D mesh animation and face animation are special cases of BIFS-Anim in that the coding of the respective animation parameters is specified in the Visual part of MPEG-4. These coded bitstreams are just wrapped into the BIFS-Anim stream.
In order to use the BIFS-Anim framework, we need to define an AnimationStream node in the scene, which points to the encoded parameter stream using an object-descriptor (just like in the case of a video-stream). The animation-stream decoder knows where to pass this data by means of a unique node-ID, e.g., that of the IndexedFaceSet2D node, which must be specified when setting up the animation-stream. From the node-ID, the animation-stream decoder can infer the node itself and its type. If the type is IndexedFaceSet2D, then the animation stream decoder knows that it must pass the encoded data to the 2Dmesh decoder, which in turn will update the appropriate fields of the IndexedFaceSet2D node. Texture mapping onto the IndexedFaceSet2D is similar to that in VRML and is explained in the Systems part of the standard.
Apart from providing the ability to animate generic still texture images with arbitrary synthetic motion, the 2D mesh object representation may also enable the following functionalities:
1) Video Object Compression
2) Video Object Manipulation
 Spatio-temporal interpolation: Mesh motion modeling
provides more robust motion-compensated temporal interpolation (frame rate
up-conversion).
Spatio-temporal interpolation: Mesh motion modeling
provides more robust motion-compensated temporal interpolation (frame rate
up-conversion).
Figure 25: An example of 2D augmented reality: The letters "Fishy?" are synthetically overlaid on the video object "Bream" and they move in synchronization with the natural motion of Bream [35].
3) Content-Based Video Indexing
MPEG-4 integrates synthetic and natural content in multimedia communications and documents. In particular, two types of synthetic visual objects are defined in version 1: animated faces and animated 2D meshes. MPEG-4 defines a complete set of animation parameters tailored towards animation of the human face. In order to enable animation of a face model over low bitrate communication channels, for point to point as well as multi-point connections, MPEG-4 encodes the facial animation parameters using temporal prediction. Face models can be animated with a data rate of 300 - 2000bits/s. MPEG-4 also defines an application program interface for TTS synthesizer. Using this interface, the synthesizer can be used to provide phonemes and related timing information to the face model. This allows for animated talking heads driven just by one text stream.
2D meshes provide means to represent and/or animate generic 2D objects. MPEG-4 version-1 accommodates both uniform and Delaunay 2-D meshes. 2-D meshes with arbitrary topology can be realized as a special case of 3D generic meshes (which will become available in MPEG-4 version 2) and can be animated using the BIFS-Anim elementary stream. Experimental results indicate that coding efficiency of the 2D dynamic mesh representation (for uniform and Delaunay meshes) described in this paper is significantly better when compared to that of 2D generic mesh animation using BIFS-Anim.
It is important to note that both face animation and 2D mesh animation may be used as representations of real video objects for highly efficient compression (model-based coding) or to generate completely synthetic video objects (virtual or augmented reality). Of course, the model-based coding application requires powerful video object analysis tools to estimate the animation parameters that would imitate real video objects.
Acknowledgements:
The authors would like to thank Dr. Peter van Beek for his contributions and Prof. Yao Wang and Prof. F. Pereira for their review of the manuscript.
[1] S. Morishima and H. Harashima, "A Media Conversion from Speech to Facial Image for Intelligent Man-Machine Interface", IEEE Jou. Selected Areas in Communications, vol. 9, no. 4, pp. 594-600, May 1991.
[2] Kalra P., Mangili A, Magnenat-Thalmann N, Thalmann D. "Simulation of Facial Muscle Actions Based on Rational Free Form Deformations", Proc. Eurographics 92, pp. 59-69, 1992.
[3] R. Sproat and J. Olive, "An Approach To Text-to-speech Synthesis", In W.B. Kleijn & K.K. Paliwal (Eds.) Speech Coding and Synthesis, Elsevier Science, 1995.
[4] F. I. Parke, "Parameterized Models for Facial Animation", IEEE Computer Graphics and Applications, vol. 2, pp. 61-68, Nov. 1982.
[5] M. M. Cohen and D. W. Massaro, Modeling Coarticulation in Synthetic Visual Speech, In M. Thalmann & D. Thalmann (Eds.) Computer Animation '93, Tokyo: Springer-Verlag.
[6] K. Waters and T. Levergood, "An automatic lip-synchronization algorithm for synthetic faces", Proc. of the Multimedia Conference, pages 149-156, San Francisco, California, September 1994. ACM
[7] J. Ostermann and E. Haratsch, "An animation definition interface: Rapid design of MPEG-4 compliant animated faces and bodies", International Workshop on synthetic - natural hybrid coding and three dimensional imaging, pp. 216-219, Rhodes, Greece, September 5-9, 1997.
[8] C. Bregler, M. Covell, and M. Slaney, "Video Rewrite: Driving Visual Speech with Audio", Proc. ACM SIGGRAPH 97, in Computer Graphics Proceedings, Annual Conference Series, 1997.
[9] D. Terzopolous and K. Waters, "Physically-based facial modeling, analysis and animation", Jou. of Visualization and Computer Animation, vol. 1, pp. 73-80, 1990.
[10] K. Waters, "A muscle model of animating three dimensional facial expression", Computer Graphics, Vol. 22, No. 4, pp. 17-24, 1987.
[11] J. Hartman and J. Wernecke, The VRML handbook, Addison Wesley, 1996.
[12] ISO/IEC 14772-1: 1997, Information Technology – Computer graphics and image processing – The Virtual Reality Modeling Language – Part 1: Functional specification and UTF-8 encoding.
[13] ISO/IEC IS 14496-1 Systems, 1999.
[14] ISO/IEC IS 14496-2 Visual, 1999.
[15] ISO/IEC IS 14496-3 Audio, 1999.
[16] L. Chen, J. Ostermann, and T. Huang, ``Adaptation of a generic 3D human face model to 3D range data,'' First IEEE Workshop on Multimedia Signal Processing, Wang and et al (Ed.), IEEE, Princeton, NJ, June 1997, pp. 274-279.
[17] M. Escher and N. M. Thalmann, "Automatic 3D cloning and real-time animation of a human face, Proc. Computer Animation ’97, Geneva, 1997.
[18] S. Morishima, "Modeling of facial expression and emotion for human communication system", Display, Vol. 17, pp 15-25, 1996.
[19] P. Ekman and W.V. Friesen: Manual for the facial action coding system, Consulting Psychologist Press, Inc. Palo Alto, CA, 1978.
[20] S. Murakami and H. Tadokoro, "Generation of facial expressions based on time functions", Proceedings of IWSNHC3DI, Rhodes, September 97, pp. 212-215.
[21] Gabriel Abrantes and Fernando Pereira, "MPEG-4 Facial Animation Technology: Survey, Implementation and Results", IEEE CSVT vol. 9, no. 2, pp. 290-305, 1999.
[22] J. Ostermann and M. Beutnagel, A. Fischer, Y. Wang, "Integration of talking heads and text-to-speech synthesizers for visual TTS", ICSLP 99, Australia, December 99.
[23] J. Ostermann, "Animation of synthetic faces in MPEG-4", Computer Animation 98,.Philadelphia, June pp. 49-55, 1998.
[24] F. Lavagetto and R. Pockaj, "The facial animation engine: Toward a high-level interface for the design of MPEG-4 compliant animated faces", IEEE CSVT vol. 9, no. 2, pp. 277-289, 1999.
[25] H. Tao, H.H. Chen, W. Wu, T.S. Huang, "Compression of facial animation parameters for transmission of talking heads", IEEE CSVT vol. 9, no. 2, pp. 264-276, 1999.
[26] I. Pandzic, J. Ostermann, and D. Millen, "User Evaluation: Synthetic Talking faces for Interactive Services", accepted for publication in The Visual Computer, Special Issue on Real-time Virtual Worlds, 1999.
[27] A. M. Tekalp, Digital Video Processing, Prentice Hall, 1995.
[28] M. de Berg, M. van Kreveld, M. Overmars, and O. Scharzkopf, Computational Geometry - Algorithms and Applications, Berlin, Germany: Springer, 1997.
[29] Y. Wang and J. Ostermann, "Evaluation of mesh-based motion estimation in H.263 like coders", IEEE Trans. on Circuits and Systems in Video Technology, pp. 243 – 252, 1998.
[30] Y. Nakaya and H. Harashima, "Motion compensation based on spatial transformations," IEEE Trans. Circ. and Syst for Video Technology, vol. 4, no. 3, pp. 339-356, June 1994.
[31] Y. Altunbasak and A. M. Tekalp, " Closed-form connectivity preserving solutions for motion compensation using 2-D meshes," IEEE Trans. on Image Proc., vol. 6, no. 9, pp. 1255-1269, Sept. 1997.
[32] Y. Wang and O. Lee, "Active mesh- A feature seeking and tracking image sequence representation scheme," IEEE Trans. Image Proc., vol. 3, no. 5, pp. 610-624, Sept. 1994.
[33] Y. Altunbasak and A. M. Tekalp, "Occlusion-adaptive, content-based mesh design and forward tracking," IEEE Trans. on Image Proc., vol. 6, no. 9, pp. 1270-1280, Sept. 1997.
[34] C. Toklu, A. T. Erdem, M. I. Sezan, and A. M. Tekalp, "Tracking motion and intensity variations using ierarchical 2-D mesh modeling," Graphical Models and Image Processing, vol. 58, no. 6, pp. 553-573, Nov. 1996.
[35] A. M. Tekalp, P. J.L. van Beek, C. Toklu, and B. Gunsel, "Two-dimensional mesh-based visual object representation for interactive synthetic/natural digital video," Proc. of the IEEE, vol. 86, no. 6, pp. 1029-1051, June 1998.
[36] P. J.L. van Beek, A. M. Tekalp, N. Zhuang, I. Celasun, and M. Xia, "Hierarchical 2D mesh representation, tracking, and compression for object-based video," IEEE Trans. Circ. and Syst. for Video Tech., vol. 9, no.2, pp. 353-369, March 1999.
[37] P. E. Eren, N. Zhuang, Y. Fu, and A. M. Tekalp, "Interactive object-based analysis and manipulation of digital video," IEEE Workshop on Multimedia Signal Processing, Redondo Beach, CA, Dec. 1998.
Murat Tekalp
A. Murat Tekalp received B.S. degree in Electrical Engineering, and B.S. degree in Mathematics from Bogazici University, Istanbul, Turkey in 1980, with the highest honors, and M.S. and Ph.D. degrees in Electrical, Computer and Systems Engineering from Rensselaer Polytechnic Institute (RPI), Troy, New York, in 1982 and 1984, respectively. From December 1984 to August 1987, he was a research scientist, and then a senior research scientist at Eastman Kodak Company, Rochester, New York. He joined the Electrical Engineering Department at the University of Rochester, Rochester, New York, as an Assistant Professor in September 1987, where he is currently a Professor. His current research interests are in the area of digital image and video processing, including object-based video representations, motion tracking, image/video segmentation, video filtering and restoration, image/video compression, and multimedia content description.
Prof. Tekalp is a senior member of IEEE, and a member of Sigma Xi. He received the NSF Research Initiation Award in 1988, Fulbright Scholar Award in 1999, and named as Distinguished Lecturer by IEEE Signal Processing Society in 1998. He is listed in Marquis Who'sWho in America Science and Engineering, 4th and 5th editions, and Who'sWho in the World, 17th Edition. He has chaired the IEEE Signal Processing Society Technical Committee on Image and Multidimensional Signal Processing (Jan. 1996 - Dec. 1997). He has served as an Associate Editor for the IEEE Trans. on Signal Processing (1990-1992), and IEEE Trans. on Image Processing (1994-1996). He has also been guest editor for recent special issues of Proceedings of the IEEE (on Multimedia Signal Processing, May/June 1998), IEEE Transactions on Image Processing (on Image and Video Processing for Digital Libraries, to appear), Signal Processing: Image Communications (on Real-Time Video over the Internet, September 1999). At present, he is on the editorial boards of Academic Journals Graphical Models and Image Processing, and Visual Communication and Image Representation, and the EURASIP journal on Signal Processing: Image Communication. He is also an Associate Editor for the Kluwer Journal Multidimensional Systems and Signal Processing. He was appointed as the Technical Program Chair for the 1991 IEEE Signal Processing Society Workshop on Image and Multidimensional Signal Processing, the Special Sessions Chair for the 1995 IEEE International Conference on Image Processing, and the Technical Program Co-Chair for IEEE ICASSP 2000 (to be held in Istanbul, Turkey). He is the founder and first Chairman of the Rochester Chapter of the IEEE Signal Processing Society. He was elected as the Chair of the Rochester Section of IEEE in 1994-1995. Dr. Tekalp is the author of the Prentice Hall book Digital Video Processing (1995).
Jörn Ostermann
Jörn Ostermann studied Electrical Engineering and Communications Engineering at the University of Hannover and Imperial College London, respectively. He received Dipl.-Ing. and Dr.-Ing. from the University of Hannover in 1988 and 1994, respectively.
From 1988 till 1994, he worked as a Research Assistant at the Institut für Theoretische Nachrichtentechnik conducting research in low bit-rate and object-based analysis-synthesis video coding. In 1994 and 1995 he worked in the Visual Communications Research Department at AT&T Bell Labs. He has been working with Image Processing and Technology Research within AT&T Labs - Research since 1996.
From 1993 to 1994, he chaired the European COST 211 sim group coordinating research in low bitrate video coding. Within MPEG-4, he organized the evaluation of video tools to start defining the standard. Currently, he chairs the Adhoc Group on Coding of Arbitrarily-shaped Objects in MPEG-4 Video. Jörn was a scholar of the German National Foundation.
In 1998, he received the AT&T Standards Recognition Award and the ISO award. He is a member of IEEE, the IEEE Technical Committee on Multimedia Signal Processing, and the IEEE CAS Visual Signal Processing and Communications (VSPC) Technical Committee.
His current research interests are video coding, computer vision, 3D modeling, face animation, coarticulation of acoustic and visual speech, computer-human interfaces, and speech synthesis.
Table 6: Location of feature points on a face model (Figure 2). Recommended location constraints define for some or all coordinates of a feature point the value as a function of other feature points, i.e., feature points 2.1, 2.2, 2.3 and 7.1 have the same x-coordinate thus locating them in the same yz-plane.
| Feature points | Recommended location constraints | |||
|
# |
Text description | x | y | z |
|
2.1 |
Bottom of the chin | 7.1.x | ||
|
2.2 |
Middle point of inner upper lip contour | 7.1.x | ||
|
2.3 |
Middle point of inner lower lip contour | 7.1.x | ||
|
2.4 |
Left corner of inner lip contour | |||
|
2.5 |
Right corner of inner lip contour | |||
|
2.6 |
Midpoint between f.p. 2.2 and 2.4 in the inner upper lip contour | (2.2.x+2.4.x)/2 | ||
|
2.7 |
Midpoint between f.p. 2.2 and 2.5 in the inner upper lip contour | (2.2.x+2.5.x)/2 | ||
|
2.8 |
Midpoint between f.p. 2.3 and 2.4 in the inner lower lip contour | (2.3.x+2.4.x)/2 | ||
|
2.9 |
Midpoint between f.p. 2.3 and 2.5 in the inner lower lip contour | (2.3.x+2.5.x)/2 | ||
|
2.10 |
Chin boss | 7.1.x | ||
|
2.11 |
Chin left corner | > 8.7.x and < 8.3.x | ||
|
2.12 |
Chin right corner | > 8.4.x and < 8.8.x | ||
|
2.13 |
Left corner of jaw bone | |||
|
2.14 |
Right corner of jaw bone | |||
|
3.1 |
Center of upper inner left eyelid | (3.7.x+3.11.x)/2 | ||
|
3.2 |
Center of upper inner right eyelid | (3.8.x+3.12.x)/2 | ||
|
3.3 |
Center of lower inner left eyelid | (3.7.x+3.11.x)/2 | ||
|
3.4 |
Center of lower inner right eyelid | (3.8.x+3.12.x)/2 | ||
|
3.5 |
Center of the pupil of left eye | |||
|
3.6 |
Center of the pupil of right eye | |||
|
3.7 |
Left corner of left eye | |||
|
3.8 |
Left corner of right eye | |||
|
3.9 |
Center of lower outer left eyelid | (3.7.x+3.11.x)/2 | ||
|
3.10 |
Center of lower outer right eyelid | (3.7.x+3.11.x)/2 | ||
|
3.11 |
Right corner of left eye | |||
|
3.12 |
Right corner of right eye | |||
|
3.13 |
Center of upper outer left eyelid | (3.8.x+3.12.x)/2 | ||
|
3.14 |
Center of upper outer right eyelid | (3.8.x+3.12.x)/2 | ||
|
4.1 |
Right corner of left eyebrow | |||
|
4.2 |
Left corner of right eyebrow | |||
|
4.3 |
Uppermost point of the left eyebrow | (4.1.x+4.5.x)/2 or x coord of the uppermost point of the contour | ||
|
4.4 |
Uppermost point of the right eyebrow | (4.2.x+4.6.x)/2 or x coord of the uppermost point of the contour | ||
|
4.5 |
Left corner of left eyebrow | |||
|
4.6 |
Right corner of right eyebrow | |||
|
5.1 |
Center of the left cheek | 8.3.y | ||
|
5.2 |
Center of the right cheek | 8.4.y | ||
|
5.3 |
Left cheek bone | > 3.5.x and < 3.7.x | > 9.15.y and < 9.12.y | |
|
5.4 |
Right cheek bone | > 3.6.x and < 3.12.x | > 9.15.y and < 9.12.y | |
|
6.1 |
Tip of the tongue | 7.1.x | ||
|
6.2 |
Center of the tongue body | 7.1.x | ||
|
6.3 |
Left border of the tongue | 6.2.z | ||
|
6.4 |
Right border of the tongue | 6.2.z | ||
|
7.1 |
top of spine (center of head rotation) | |||
|
8.1 |
Middle point of outer upper lip contour | 7.1.x | ||
|
8.2 |
Middle point of outer lower lip contour | 7.1.x | ||
|
8.3 |
Left corner of outer lip contour | |||
|
8.4 |
Right corner of outer lip contour | |||
|
8.5 |
Midpoint between f.p. 8.3 and 8.1 in outer upper lip contour | (8.3.x+8.1.x)/2 | ||
|
8.6 |
Midpoint between f.p. 8.4 and 8.1 in outer upper lip contour | (8.4.x+8.1.x)/2 | ||
|
8.7 |
Midpoint between f.p. 8.3 and 8.2 in outer lower lip contour | (8.3.x+8.2.x)/2 | ||
|
8.8 |
Midpoint between f.p. 8.4 and 8.2 in outer lower lip contour | (8.4.x+8.2.x)/2 | ||
|
8.9 |
Right hiph point of Cupid’s bow | |||
|
8.10 |
Left hiph point of Cupid’s bow | |||
|
9.1 |
Left nostril border | |||
|
9.2 |
Right nostril border | |||
|
9.3 |
Nose tip | 7.1.x | ||
|
9.4 |
Bottom right edge of nose | |||
|
9.5 |
Bottom left edge of nose | |||
|
9.6 |
Right upper edge of nose bone | |||
|
9.7 |
Left upper edge of nose bone | |||
|
9.8 |
Top of the upper teeth | 7.1.x | ||
|
9.9 |
Bottom of the lower teeth | 7.1.x | ||
|
9.10 |
Bottom of the upper teeth | 7.1.x | ||
|
9.11 |
Top of the lower teeth | 7.1.x | ||
|
9.12 |
Middle lower edge of nose bone (or nose bump) | 7.1.x | (9.6.y + 9.3.y)/2 or nose bump | |
|
9.13 |
Left lower edge of nose bone | (9.6.y +9.3.y)/2 | ||
|
9.14 |
Right lower edge of nose bone | (9.6.y +9.3.y)/2 | ||
|
9.15 |
Bottom middle edge of nose | 7.1.x | ||
|
10.1 |
Top of left ear | |||
|
10.2 |
Top of right ear | |||
|
10.3 |
Back of left ear | (10.1.y+10.5.y)/2 | ||
|
10.4 |
Back of right ear | (10.2.y+10.6.y)/2 | ||
|
10.5 |
Bottom of left ear lobe | |||
|
10.6 |
Bottom of right ear lobe | |||
|
10.7 |
Lower contact point between left lobe and face | |||
|
10.8 |
Lower contact point between right lobe and face | |||
|
10.9 |
Upper contact point between left ear and face | |||
|
10.10 |
Upper contact point between right ear and face | |||
|
11.1 |
Middle border between hair and forehead | 7.1.x | ||
|
11.2 |
Right border between hair and forehead | < 4.4.x | ||
|
11.3 |
Left border between hair and forehead | > 4.3.x | ||
|
11.4 |
Top of skull | 7.1.x | > 10.4.z and < 10.2.z | |
|
11.5 |
Hair thickness over f.p. 11.4 | 11.4.x | 11.4.z | |
|
11.6 |
Back of skull | 7.1.x | 3.5.y | |
Table 7: FAP definitions, group assignments, and step sizes. FAP names may contain letters with the following meaning: l = left, r = right, t = top, b = bottom, i = inner, o = outer, m = middle. The quantizer step-size is a scaling factor for coding as described in Section 2.2.
|
# |
FAP name |
FAP description |
units |
Uni-orBidir |
Pos motion |
G |
FDP subgrp num |
Quant step size QP |
Min/Max I-Frame quantized values |
Min/Max P-Frame quantized values |
|
1 |
viseme |
Set of values determining the mixture of two visemes for this frame (e.g. pbm, fv, th) |
na |
na |
na |
1 |
na |
1 |
viseme_blend: +63 |
viseme_blend: +-63 |
|
2 |
expression |
A set of values determining the mixture of two facial expression |
na |
na |
na |
1 |
na |
1 |
expression_intensity1, expression_intensity2: +63 |
expression_intensity1, expression_intensity2: +-63 |
|
3 |
open_jaw |
Vertical jaw displacement (does not affect mouth opening) |
MNS |
U |
down |
2 |
1 |
4 |
+1080 |
+360 |
|
4 |
lower_t_midlip |
Vertical top middle inner lip displacement |
MNS |
B |
down |
2 |
2 |
2 |
+-600 |
+-180 |
|
5 |
raise_b_midlip |
Vertical bottom middle inner lip displacement |
MNS |
B |
up |
2 |
3 |
2 |
+-1860 |
+-600 |
|
6 |
stretch_l_cornerlip |
Horizontal displacement of left inner lip corner |
MW |
B |
left |
2 |
4 |
2 |
+-600 |
+-180 |
|
7 |
stretch_r_cornerlip |
Horizontal displacement of right inner lip corner |
MW |
B |
right |
2 |
5 |
2 |
+-600 |
+-180 |
|
8 |
lower_t_lip_lm |
Vertical displacement of midpoint between left corner and middle of top inner lip |
MNS |
B |
down |
2 |
6 |
2 |
+-600 |
+-180 |
|
9 |
lower_t_lip_rm |
Vertical displacement of midpoint between right corner and middle of top inner lip |
MNS |
B |
down |
2 |
7 |
2 |
+-600 |
+-180 |
|
10 |
raise_b_lip_lm |
Vertical displacement of midpoint between left corner and middle of bottom inner lip |
MNS |
B |
up |
2 |
8 |
2 |
+-1860 |
+-600 |
|
11 |
raise_b_lip_rm |
Vertical displacement of midpoint between right corner and middle of bottom inner lip |
MNS |
B |
up |
2 |
9 |
2 |
+-1860 |
+-600 |
|
12 |
raise_l_cornerlip |
Vertical displacement of left inner lip corner |
MNS |
B |
up |
2 |
4 |
2 |
+-600 |
+-180 |
|
13 |
raise_r_cornerlip |
Vertical displacement of right inner lip corner |
MNS |
B |
up |
2 |
5 |
2 |
+-600 |
+-180 |
|
14 |
thrust_jaw |
Depth displacement of jaw |
MNS |
U |
forward |
2 |
1 |
1 |
+600 |
+180 |
|
15 |
shift_jaw |
Side to side displacement of jaw |
MW |
B |
right |
2 |
1 |
1 |
+-1080 |
+-360 |
|
16 |
push_b_lip |
Depth displacement of bottom middle lip |
MNS |
B |
forward |
2 |
3 |
1 |
+-1080 |
+-360 |
|
17 |
push_t_lip |
Depth displacement of top middle lip |
MNS |
B |
forward |
2 |
2 |
1 |
+-1080 |
+-360 |
|
18 |
depress_chin |
Upward and compressing movement of
the chin
(like in sadness) |
MNS |
B |
up |
2 |
10 |
1 |
+-420 |
+-180 |
|
19 |
close_t_l_eyelid |
Vertical displacement of top left eyelid |
IRISD |
B |
down |
3 |
1 |
1 |
+-1080 |
+-600 |
|
20 |
close_t_r_eyelid |
Vertical displacement of top right eyelid |
IRISD |
B |
down |
3 |
2 |
1 |
+-1080 |
+-600 |
|
21 |
close_b_l_eyelid |
Vertical displacement of bottom left eyelid |
IRISD |
B |
up |
3 |
3 |
1 |
+-600 |
+-240 |
|
22 |
close_b_r_eyelid |
Vertical displacement of bottom right eyelid |
IRISD |
B |
up |
3 |
4 |
1 |
+-600 |
+-240 |
|
23 |
yaw_l_eyeball |
Horizontal orientation of left eyeball |
AU |
B |
left |
3 |
na |
128 |
+-1200 |
+-420 |
|
24 |
yaw_r_eyeball |
Horizontal orientation of right eyeball |
AU |
B |
left |
3 |
na |
128 |
+-1200 |
+-420 |
|
25 |
pitch_l_eyeball |
Vertical orientation of left eyeball |
AU |
B |
down |
3 |
na |
128 |
+-900 |
+-300 |
|
26 |
pitch_r_eyeball |
Vertical orientation of right eyeball |
AU |
B |
down |
3 |
na |
128 |
+-900 |
+-300 |
|
27 |
thrust_l_eyeball |
Depth displacement of left eyeball |
ES |
B |
forward |
3 |
na |
1 |
+-600 |
+-180 |
|
28 |
thrust_r_eyeball |
Depth displacement of right eyeball |
ES |
B |
forward |
3 |
na |
1 |
+-600 |
+-180 |
|
29 |
dilate_l_pupil |
Dilation of left pupil |
IRISD |
B |
growing |
3 |
5 |
1 |
+-420 |
+-120 |
|
30 |
dilate_r_pupil |
Dilation of right pupil |
IRISD |
B |
growing |
3 |
6 |
1 |
+-420 |
+-120 |
|
31 |
raise_l_i_eyebrow |
Vertical displacement of left inner eyebrow |
ENS |
B |
up |
4 |
1 |
2 |
+-900 |
+-360 |
|
32 |
raise_r_i_eyebrow |
Vertical displacement of right inner eyebrow |
ENS |
B |
up |
4 |
2 |
2 |
+-900 |
+-360 |
|
33 |
raise_l_m_eyebrow |
Vertical displacement of left middle eyebrow |
ENS |
B |
up |
4 |
3 |
2 |
+-900 |
+-360 |
|
34 |
raise_r_m_eyebrow |
Vertical displacement of right middle eyebrow |
ENS |
B |
up |
4 |
4 |
2 |
+-900 |
+-360 |
|
35 |
raise_l_o_eyebrow |
Vertical displacement of left outer eyebrow |
ENS |
B |
up |
4 |
5 |
2 |
+-900 |
+-360 |
|
36 |
raise_r_o_eyebrow |
Vertical displacement of right outer eyebrow |
ENS |
B |
up |
4 |
6 |
2 |
+-900 |
+-360 |
|
37 |
squeeze_l_eyebrow |
Horizontal displacement of left eyebrow |
ES |
B |
right |
4 |
1 |
1 |
+-900 |
+-300 |
|
38 |
squeeze_r_eyebrow |
Horizontal displacement of right eyebrow |
ES |
B |
left |
4 |
2 |
1 |
+-900 |
+-300 |
|
39 |
puff_l_cheek |
Horizontal displacement of left cheeck |
ES |
B |
left |
5 |
1 |
2 |
+-900 |
+-300 |
|
40 |
puff_r_cheek |
Horizontal displacement of right cheeck |
ES |
B |
right |
5 |
2 |
2 |
+-900 |
+-300 |
|
41 |
lift_l_cheek |
Vertical displacement of left cheek |
ENS |
U |
up |
5 |
3 |
2 |
+-600 |
+-180 |
|
42 |
lift_r_cheek |
Vertical displacement of right cheek |
ENS |
U |
up |
5 |
4 |
2 |
+-600 |
+-180 |
|
43 |
shift_tongue_tip |
Horizontal displacement of tongue tip |
MW |
B |
right |
6 |
1 |
1 |
+-1080 |
+-420 |
|
44 |
raise_tongue_tip |
Vertical displacement of tongue tip |
MNS |
B |
up |
6 |
1 |
1 |
+-1080 |
+-420 |
|
45 |
thrust_tongue_tip |
Depth displacement of tongue tip |
MW |
B |
forward |
6 |
1 |
1 |
+-1080 |
+-420 |
|
46 |
raise_tongue |
Vertical displacement of tongue |
MNS |
B |
up |
6 |
2 |
1 |
+-1080 |
+-420 |
|
47 |
tongue_roll |
Rolling of the tongue into U shape |
AU |
U |
concave |
6 |
3, 4 |
512 |
+300 |
+60 |
|
48 |
head_pitch |
Head pitch angle from top of spine |
AU |
B |
down |
7 |
na |
170 |
+-1860 |
+-600 |
|
49 |
head_yaw |
Head yaw angle from top of spine |
AU |
B |
left |
7 |
na |
170 |
+-1860 |
+-600 |
|
50 |
head_roll |
Head roll angle from top of spine |
AU |
B |
right |
7 |
na |
170 |
+-1860 |
+-600 |
|
51 |
lower_t_midlip _o |
Vertical top middle outer lip displacement |
MNS |
B |
down |
8 |
1 |
2 |
+-600 |
+-180 |
|
52 |
raise_b_midlip_o |
Vertical bottom middle outer lip displacement |
MNS |
B |
up |
8 |
2 |
2 |
+-1860 |
+-600 |
|
53 |
stretch_l_cornerlip_o |
Horizontal displacement of left outer lip corner |
MW |
B |
left |
8 |
3 |
2 |
+-600 |
+-180 |
|
54 |
stretch_r_cornerlip_o |
Horizontal displacement of right outer lip corner |
MW |
B |
right |
8 |
4 |
2 |
+-600 |
+-180 |
|
55 |
lower_t_lip_lm _o |
Vertical displacement of midpoint between left corner and middle of top outer lip |
MNS |
B |
down |
8 |
5 |
2 |
+-600 |
+-180 |
|
56 |
lower_t_lip_rm _o |
Vertical displacement of midpoint between right corner and middle of top outer lip |
MNS |
B |
down |
8 |
6 |
2 |
+-600 |
+-180 |
|
57 |
raise_b_lip_lm_o |
Vertical displacement of midpoint between left corner and middle of bottom outer lip |
MNS |
B |
up |
8 |
7 |
2 |
+-1860 |
+-600 |
|
58 |
raise_b_lip_rm_o |
Vertical displacement of midpoint between right corner and middle of bottom outer lip |
MNS |
B |
up |
8 |
8 |
2 |
+-1860 |
+-600 |
|
59 |
raise_l_cornerlip_o |
Vertical displacement of left outer lip corner |
MNS |
B |
up |
8 |
3 |
2 |
+-600 |
+-180 |
|
60 |
raise_r_cornerlip _o |
Vertical displacement of right outer lip corner |
MNS |
B |
up |
8 |
4 |
2 |
+-600 |
+-180 |
|
61 |
stretch_l_nose |
Horizontal displacement of left side of nose |
ENS |
B |
left |
9 |
1 |
1 |
+-540 |
+-120 |
|
62 |
stretch_r_nose |
Horizontal displacement of right side of nose |
ENS |
B |
right |
9 |
2 |
1 |
+-540 |
+-120 |
|
63 |
raise_nose |
Vertical displacement of nose tip |
ENS |
B |
up |
9 |
3 |
1 |
+-680 |
+-180 |
|
64 |
bend_nose |
Horizontal displacement of nose tip |
ENS |
B |
right |
9 |
3 |
1 |
+-900 |
+-180 |
|
65 |
raise_l_ear |
Vertical displacement of left ear |
ENS |
B |
up |
10 |
1 |
1 |
+-900 |
+-240 |
|
66 |
raise_r_ear |
Vertical displacement of right ear |
ENS |
B |
up |
10 |
2 |
1 |
+-900 |
+-240 |
|
67 |
pull_l_ear |
Horizontal displacement of left ear |
ENS |
B |
left |
10 |
3 |
1 |
+-900 |
+-300 |
|
68 |
pull_r_ear |
Horizontal displacement of right ear |
ENS |
B |
right |
10 |
4 |
1 |
+-900 |
+-300 |